I/D 1 Unit N Concepts

1. A triangle with one right angle is called a right triangle. The side opposite the right angle is called the hypotenuse of the triangle. The other two sides are called legs. The other two angles have no special name, but they are always complementary. Do you see why? The total angle sum of a triangle is 180 degrees, and the right angle is 90 degrees, so the other two must sum to 90 degrees. One is the right triangle formed when an altitude is drawn from a vertex of an equilateral triangle, forming two congruent right triangles. The angles of the triangle will be 30, 60, and 90 degrees, giving the triangle its name: 30-60-90 triangle. The ratio of side lengths in such triangles is always the same: if the leg opposite the 30 degree angle is of length x , the leg opposite the 60 degree angle will be of x , and the hypotenuse across from the right angle will be 2x . Here is a 30-60-90 triangle pictured below. Which side is which? The side opposite the 30 degree angle will have the shortest length. The side opposite the 60 degree angle will be sqrt(3) times as long, and the side opposite the 90 degree angle will be twice as long. The triangle below diagrams this relationship.

30-60-90 triangle side ratios proof: Proving the ratios between the sides of a 30-60-90 triangle

(http://www.khanacademy.org/math/geometry/right_triangles_topic/special_right_triangles/v/30-60-90-triangle-side-ratios-proof)

2. 45-45-90 triangle side ratios: Showing the ratios of the sides of a 45-45-90 triangle are 1:1:sqrt(2)

(http://www.khanacademy.org/math/geometry/right_triangles_topic/special_right_triangles/v/45-45-90-triangle-side-ratios)

The other common right triangle results from the pair of triangles created when a diagonal divides a square into two triangles. Each of these triangles is congruent, and has angles of measures 45, 45, and 90 degrees. If the legs opposite the 45 degree angles are of length x , the hypotenuse has a length of x 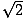. This ratio holds true for all 45-45-90 triangles. 45-45-90 triangles are also often called isosceles right triangles.

3.

4.This Activity help us derive the unit circle by knowing the lengths . of we forget something about the unit circle